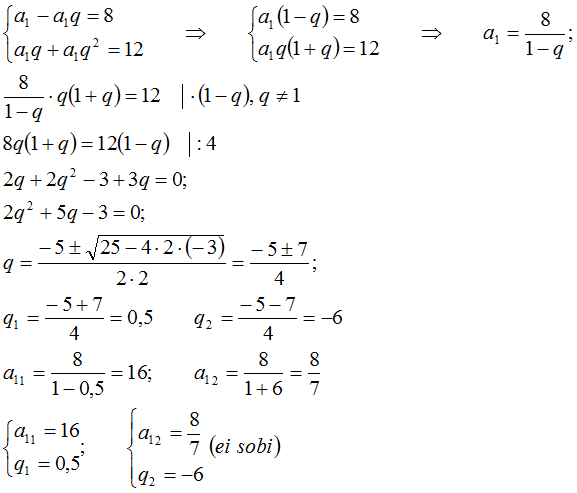Käin 11 klassis ning sain matemaatikas koduse kontrolltöö, mida ma kahjuks üldse ei oska -.-
1) Aritmeetilise jada viimane liige on 31, eelviimase ja teise liikme summa on 34 ning liikmete arv võrdub esimese ja teise liikme korrutisega. Leia jada liikmete summa
2) Punkt liikus sirgjooneliselt esimese sekundiga 8m ja iga järgneva sekundiga 2 meetri võrra rohkem kui eelnevaga. Samaaegselt hakkas talle 140 meetri kauguselt vastu liikuma punkt kiirusega 16 m/s. mitme sekundi pärast need punktid kohtuvad?
3) Leia geomeetriline jada, mille summa on 243 ja esimese viie liikme summa 275
4) Leia neli arvu, mis moodustavad geomeetrilise jada, kui äärmiste arvude vahe on 19 ja keskmiste arvude vahe 6.
5) Neli arvu moodustavad geomeetrilise jada. Kui teise arvuga liita 4 ja kolmandaga 5, siis saadud neli arvu moodustavad aritmeetilise jada. Leia arvud, mis moodustavad aritmeetilise jada.
6) Hääbuva geomeetrilise jada esimese ja teise liikme vahe on 8, teise ja kolmanda liikme summa aga 12. Keua selle jada kolm liiget.
7) leia jada piirväärtus n->lõpmatus kui an=2n-ruutjuur(4n ruudus -3n-1)

Soovin, et keegi kasvõi natukene aitaks ;)
Ette tänades mustkass








 Tagasi üles
Tagasi üles